|
| MegaPrime/MegaCam Home |
| CFHT Home |
| General Information |
| Instrument Description |
| Press Release April 8, 2003 |
| Publications |
| Acknowledgment Text |
| Specifications & Performance |
| Quick Performance Summary |
| General Summary |
| Technical Considerations |
| Off-field bright stars immunity |
| Shutter ballistics |
| Baffling & pinhole mask |
| On-sky Instrument History |
| Observing Runs |
| Observing Statistics |
| Observing Statistics II |
| Upgrades & Problems |
| Zeropoint History |
| New Observing Process |
| Exposure Time Calculator |
| Mapping Stars & Pointings |
| Queued Service Observing |
| QSO PH2 |
| SkyProbe |
| Data Preprocessing & Calibration |
| Elixir System Information |
| Raw Data Description |
| CFHT Data Preprocessing |
| CFHT Data Calibration |
| CFHT MetaData Products |
| Raw & Elixir FITS headers |
| Elixir Releases History |
| Elixir Real-Time |
| Elixir RT Field Guide |
| Elixir RT Status |
| Flat-Fields Status |
| Standards Status |
| Instrument Operations |
| Cooling Status |
| Cryostat Status |
| External Related Sites |
| Data Archiving at CADC |
| Data Processing at Terapix |
| Contacts |
| Support Astronomer |
| Technical considerations to prepare MegaCam observations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table of contents:
IntroductionThis page provides information of interest to the observer preparing MegaCam observations. Like CFH12K before it, MegaCam is operated in Queued Service Observing mode. However, in the case of MegaCam, classical observing is not offered to observers. Observers will receive their MegaCam data after pre-processing (and astrometric and photometric calibration on a per CCD basis) by the CFHT Elixir analysis system, though they may request raw data if necessary.This page follows the structure of the various sections found in the "General Summary" table and provides further details related to the impact they may have on an observing strategy. Starting 2015A, Megacam has a new set of broad and narrow band filters with a larger foot print than the old broad band filters, therefore allowing to observe with all 40 CCDs (see below).
The old filters (u 1 Geometry1.1 Mosaic organizationAlthough the camera is read through all 80 amplifiers (two per detector), the data is re-organized at CFHT to splice amplifiers from the same detector into a single FITS image (a process we call "splicing"). Figure 1 shows the organization of the readout amplifiers within the focal plane. The final extension name is given on the CCD (00 to 39). After the splicing process (done on the fly - the raw data are the spliced data) all detectors have their pixel {X=1, Y=1} near the A amplifier, i.e. as if all the detectors in the mosaic had been read from the A amplifier. Note that the physical gaps in the mosaic are not represented on this figure. For data before 2015A, only CCDs 00-35 were used, and for data starting with 2015A, all CCDs are in use. The CCDs labeled 36,37,38,39 are referred to as the 'ears'.
1.2 Wide-Field Corrector optical distortionThere is a significant optical distortion beyond a 20 arcminutes radius and one should be aware than creating large monolithic images from a stack of dithered exposures will require a global resampling. The Terapix Data Center will provide this service to the CFHT community (the tool developed for that very function is called "swarp").Nevertheless, depending on the scientific goals, recovering the medium (13 arcsec wide, or 70 pixels) and large (80 arcsec wide, or 425 pixels) gaps in the mosaic is not always a necessity. For that reason, three types of dithering pattern are offered in the QSO interface:
1.3 Evaluation of the image quality across the field of viewThe new wide-field corrector was expected to cause an image degradation from center to edge of less than 0.1 arcsecond. One should be aware than when requesting a given image quality, it is assumed as being the image quality from the center region of the mosaic. Hence, if 1.0 arcsecond is required over the whole field of view, one should request an image quality of 0.9".We have defined image quality estimators to quantify this effect on the observed image. They rely on ratio of image quality measurements between various regions (shown on Figure 3) of the mosaic.
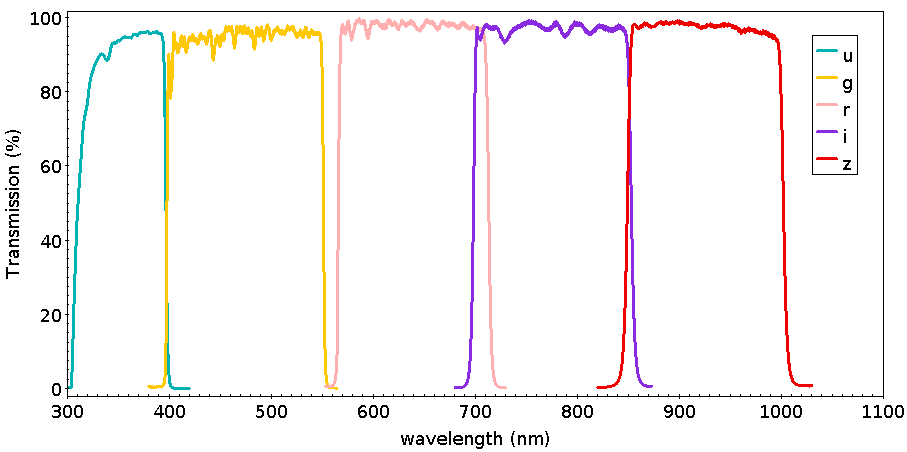
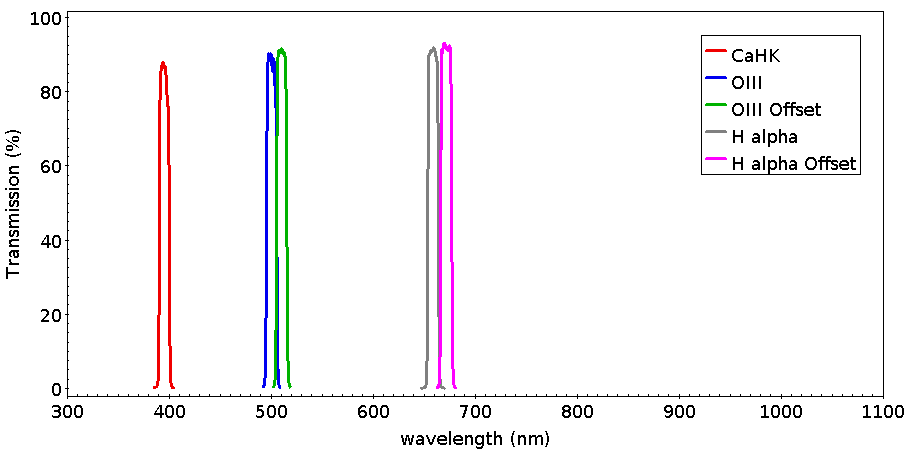
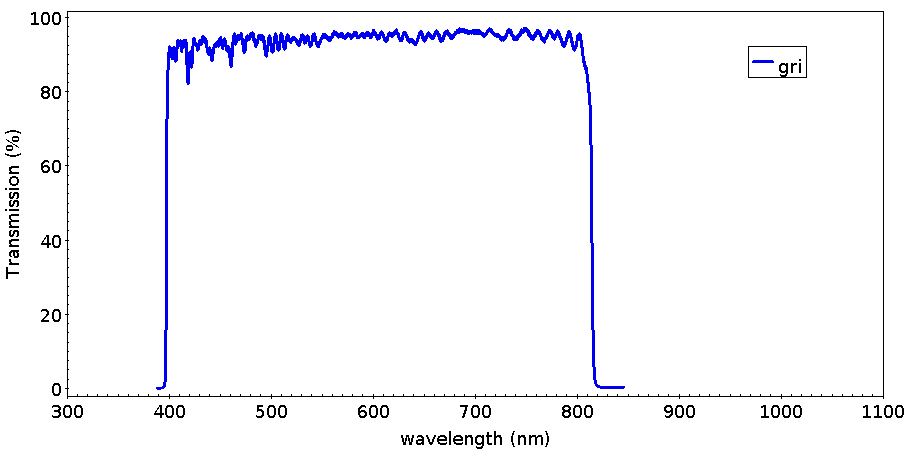
IMAGE: 712976 ------------------ IQ MAP & CLASS TO MEDIAN 1-9 | *0 |+/-1|+/-2|+/-3|+/-4|+/-5|+/-6|+/-7|+/-8|+/-9| IQ difference in arcsec ---> <0.02<0.06<0.11<0.17<0.22<0.28<0.34<0.39<0.41< more |0.81|0.77|0.74|0.74|0.72|0.73|0.76|0.82|0.88| |+1|*0|*0|-1|-1|-1|*0|+2|+3| |0.80|0.75|0.69|0.67|0.67|0.68|0.70|0.74|0.80| |+1|*0|-2|-2|-2|-2|-2|-1|+1| |0.83|0.77|0.71|0.68|0.68|0.70|0.72|0.76|0.82| |+2|*0|-1|-2|-2|-2|-1|*0|+2| |0.90|0.84|0.80|0.77|0.77|0.77|0.80|0.85|0.93| |+3|+2|+1|*0|*0|*0|+1|+2|+4| CENTER = 0.69" OUTER RING = 0.79" RADIUS R = 1.144 [ center / (top+left+bottom+right) ] PISTON X = 1.018 [ right / left ] PISTON Y = 0.937 [ top / bottom ]MegaCam is focused (and soon autofocused) for the position that optimizes the image quality over the entire mosaic (optimal focus at the center would cause greater degradation on the edges). 2 Photometry2.1 Current filter setMegaCam has 11 filters in use since 2015A. These are named u, g, r, i, z for the new broad band filters, gri for a wide band filter, and Ha, HaOFF, OIII, OIIIOFF and CaHK for the narrow band filters. Due to their larger foot print, these filters allow a full (unvignetted) illumination of the 40 CCDs of the mosaic .
The following table gives basic filter charateristics for the current set of filters. The measured
mean bandwidth and mean transmission over that bandwidth are derived from scans performed at CFHT for each filter.
Note that the ETC is now available also for the new filters, however, due to the current lack of statistics, values for sky background and airmass extinction terms were deduced from their broad band counterparts. Photometric calibration is not yet available for these filters, however, all necessary standard star observations have been done, which will allow a photometric calibration to be computed for all data taken with these filters (starting from 2015A) in the near future. A summary of their properties are given in the Table below. Detailed transmission data are available here. Figures 4, 5, and 6 below show the transmission curves for all of the filters currently in use for MegaCam.
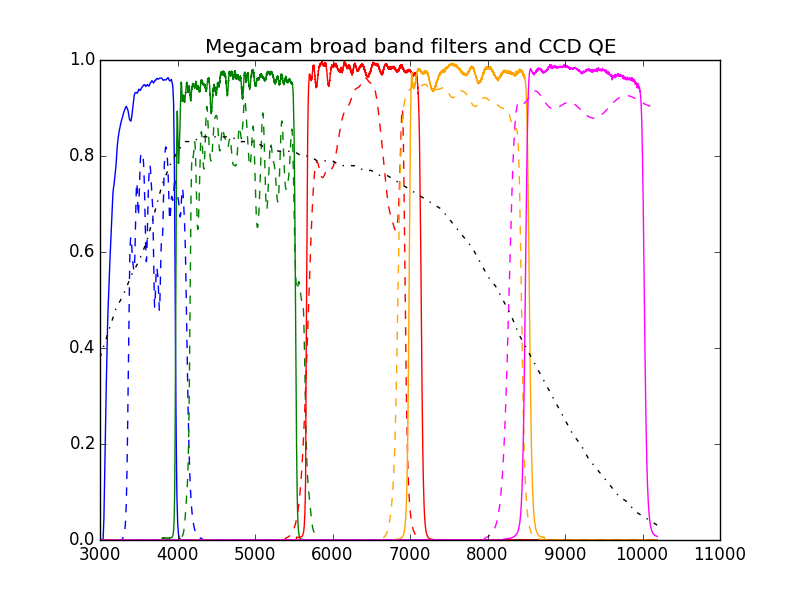
2.2 Comparison of filter setsUntil 2015A, MegaPrime used five ("old") broad-band filters, constructed by SAGEM: uStarting 2015A, these (old) filters were replaced by a new set of broad and narrow band filters , simply named u, g, r, i, z for the new broad band filters, gri for a wide band filter, and Ha, HaOFF, OIII, OIIIOFF and CaHK for the narrow band filters. Due to their larger foot print, these filters allow a full (unvignetted) illumination of the 40 CCDs of the mosaic . The plot below (Figure 7) shows the (mean) measured transmission curves of the 5 new SDSS-like filters (solid lines) as measured by their respective manufactures, Asahi for u, Materion for the others. The old filter mean transmissions (as measured at CFHT) are shown in dashed lines for comparison. The new filter transmissions are shown in solid, colored lines. Each filter was scanned 17 times by the manufacturer at different places, the mean transmission is reported in the figure. Note that the new z filter has a red cutoff and a redder blue cutoff, which explains the lower zero point compared to the old z filter. The full manufacturer scans are available here.
The following table gives basic filter charateristics for the broad band filters, old and new. The measured
mean bandwidth and mean transmission over that bandwidth are derived
from scans performed at CFHT for each filter.
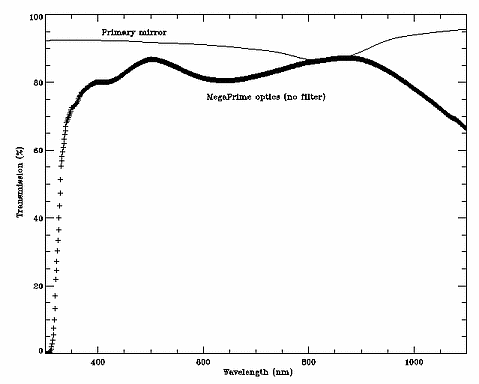
Each old filter was scanned 10 times at a range of radii and the resulting measurement have been averaged to generate the curves below. Newer data from actual filters scans are available in ASCII format here. The original scans by the manufacturer (SAGEM), which differ slightly from the CFHT scans *but which are believed to be more accurate*, can be found here. The full manufacturer scans of the current filters are available here. 2.3 Telescope and MegaPrime/MegaCam opticsThe CFHT is equiped with a 3.58 diameter mirror and MegaPrime causes an obstruction which is larger than its central hole. After adding the footprint of the primary focus and the four spider branches supporting it, the final collecting area of the primary mirror is 80,216 square centimeters (each spider branch is 5 cm wide, over the area of the primary mirror, 3 are 111.5 cm long and one is 81.5 long, the prime focus can be modeled by two circles of 67.5 cm radius each with a central bridge between their centers of 30 cm).The reflectivity model for the primary mirror is of a freshly coated, bare aluminum. The curve is shown on figure 8 and the data used to generate that plot are available here. The transmission model of the Wide-Field Corrector and the camera window is derived from combining all the transmission and diffusion effects of the various glass and coatings. The curve is shown on figure 8 and the data used to generate that plot are available here.
2.4 CCD quantum efficiencyThe following table is the average measurement of the quantum efficiency (QE) over the 40 CCDs populating the MegaCam focal plane. The dispersion at each measured wavelength is also provided and shows that there are variations from chip to chip; in consequence these numbers must be considered only to describe an average behavior of the detectors.The measurements were performed individually on each chip at CEA.
The data from this table are available in ASCII format here. A more precise table with a point every 10 nm is available here. Note that these are results from a simulation for a given set of CCD characteristics that match best the table of real measurements provided above.
2.5 Narrow band filters: old CFH12K filters (forcing a reduced field of view) and new, full mosaic filtersA set of CFH12K narrow band filters (HaS, HaOFFS, TiOS, CNS, HbS, HbOFFS, OIII) were in use until 2015A. Their characteristics are summarized in the table below.
These narrow band filters cover 14 chips at the center of the mosaic (10 to 16 and 19 to 25) though the external ones will have their external sides strongly vignetted. The resulting fielf of view is 42 by 28 square arcminutes. More information on this filter set can be found here. Starting with 2015A, a new set of narrow band filters, covering all 40 chips in the mosaic, are available for observations. Note that only the new filters (u,g,r,i,z,gri,Ha,HaOFF, OIII, OIIIOFF, and CaHK) are available for use with Megacam. Note that the ETC is now available also for the new filters, however, due to the current lack of statistics, values for sky background and airmass extinction terms were deduced from their broad band counterparts. Photometric calibration is not yet available for these filters, however, all necessary standard star observations have been done, which will allow a photometric calibration to be computed for all data taken with these filters (starting from 2015A) in the near future. A summary of their properties are given in the Table below. Detailed transmission data are available here.
2.6 AB Magnitude equation
The quantum efficiency and the gain vary slightly from CCD to CCD though they are both fairly uniform over the whole mosaic (average gain is 1.67 e-/ADU with a 0.2 dispersion) and the dispersion on QE is presented in the table in 2.3. The zero points advertised on the MegaPrime pages come from photometric frames processed by Elixir. The flat-fielding step takes care of making the zero point uniform over the entire 36 CCDs (40 for new filters) of the mosaic by applying a multiplicative factor scaled on CCD00, e.g. the response is normalized to CCD00. The result is a flat looking image with a unifom sky level but with a detection limit changing slightly from CCD to CCD due to their intrinsic differences in quantum efficiency and read noise. When applying a zero point to some Elixir processed data, one should use the gain of 1.62 by default, hence apply the equation "In ADUs" provided in the table above. 2.7 Transition from AB to Vega magnitude systemThe table below allows a translation from MegaCam AB to Vega Magnitudes.
2.8 Sky brightnessSky brightness in the various MegaCam filters was derived from the 2003A semester data, and specially from engineering nights where the sky brightness had been precisely monitored in respect to the airmass, and then later in respect of the Moon phase.The measurements were derived from data obtained exclusively in photometric conditions. The combination of cirrus and the Moon in the sky is basically impossible to predict, but the effect will be less in i and z than in u, g and r. It is remarkable that the sky retains the same brightness at zenith in the i and z band no matter what the phase of the Moon is (we tested between 0% and 70%). This demonstrate that MegaPrime is a prime grey time instrument. However the sky brightness in these two bands depend greatly on the airmass. 2.9 Fringes in the i and z bandsThe fringing level in the i band is reasonably low (6%) and is fairly well corrected by Elixir, though we noticed that we may now be facing residuals due to variations in the sky spectrum during the course of a run or even a night. The fringing level in the z band is high: 15%.MegaCam is not a great instrument to observe in the z band as the CCDs sensitivity is low at those frequencies and the sky background is very high resulting in very strong fringing. 2.10 SNLS based photometric calibrationStarting with semester 2015A, the elixir zero points are based on a comparison between observations of the SNLS deep fields obtained during each run, with the catalog of absolutely calibrated SNLS "tertiary standards" (see Betoule et al. 2013). Specific color terms have been computed to relate the new MegaCam wide band filters photometric systems to the old wide band systems using synthetic magnitudes on stellar libraries, and successfully compared to empirical measurements of these color terms (courtesy S. Gwyn.). The latter are implemented in elixir, and the photometric equations and keywords described below are included in the FITS headers of the processed data. In the following, variables in capitals correspond to FITS keywords.If we define the instrumental magnitude as m = -2.5*LOG(DN)+2.5*LOG(EXPTIME),where DN is the total count number of a source (in ADU), and is the corresponding exposure time in seconds, then the calibrated (AB, SNLS) magnitude m_snls, based on MegaCam old broad band filter ugriz set, is related to this instrumental magnitude, in a given band, by the following equation: m_snls = m + PHOT_C + PHOT_K*(AIRMASS-1) +PHOT_X*(m_snls(PHOT_C1)-m_snls(PHOT_C2))where PHOT_C is the value of the zero point in that band (current value for the camera run), PHOT_K is the extinction coefficient in that band, AIRMASS is the observation airmass, PHOT_X is the slope of the color correction, and PHOT_C1 and PHOT_C2 are the (SNLS, old Megacam broad band) bands used to define the color term. This equation assumes that these color terms are known. If one just wants the AB magnitude in the filter used for the observation, then PHOT_X can be put to zero in the equation above. Of course, if the filter used is one of the old broad band filters (used to define the SNLS photometric system), then the corresponding PHOT_X are naturally equal to zero. The following table gives the relevant information for the SNLS photometric system, and also for the SDSS 2.5m photometric system for reference. The linear color terms PHOT_X (SNLS) have been adjusted to color-color diagrams obtained from matching catalogs obtained on the SNLS deep fields, and by matching catalogs to the SDSS catalog for PHOT_X (SDSS) (courtesy S. Gwyn, see this page ).
These zero point estimates have been compared to other estimates based on the observation of spectrophotometric (CALSPEC) HST standards and their corresponding synthetic magnitudes, and have been found to be in reasonable agreement. The same HST standards and synthetic magnitudes are used to give a rough estimate of zero points for the new narrow band filters. In addition, the SNLS code (courtesy Marc Betoule) to produce superflat (photometric grid) solutions has been adapted to the new focal plane layout with 40 CCDs, and was used to produce photometric grid corrections on all new wideband filters, as well as the narrow band filters as soon as data become available. See "MegaCam photometric calibration" for details. 3 Observing3.1 Immunity to bright stars scattered lightThere are three possible ways for contamination by bright stars:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||