CFHTLS T0007 photometry is anchored to the SNLS photometric system (?) using a catalogue of tertiary standard stars supplied in this paper. This choice of calibrators implies that the filter banpasses to be used in any scientific analysis are those defined by the SNLS team and described in section 3.7.5. The method to tie the CFHTLS to the SNLS reference system follows the method described in ?:
The calibration process is different for the Wide and the Deep surveys.
The Deep stacks can be calibrated directly using SNLS tertiary standards inside the Deep fields. Zero-points can therefore be computed by comparing the instrumental magnitudes of the SNLS standard stars to the calibrated magnitudes published in ? and applying the relevant Vega to AB magnitude offset (Table 2).
However, as there is no complete coverage of SNLS tertiary standards within the Wide fields, a special set of obse

Each Wide tile is covered by at least one L99 exposure which covers 25% of the MegaCam field of view on each Wide tile. Given that the stacks are photometrically flat within 1% across the field of view due to the use of the Elixir B5/SNLS recipe, this guarantees that in turn all four quadrants are photometrically uniform.
Additionally, each L99 observation is preceded and followed by an observation of a CFHTLS Deep field containing the SNLS tertiary standards.
The photometric measurement method used to calibrate the Deep exposures taken before and after L99 observations follows the same procedure used for CFHTLS Deep stacks described above. The stable photometric conditions allows this zero-point to be used for the corresponding L99 exposures. In the last step, L99 images are used to compute rescaling factors which can be applied to the CFHTLS Wide stacks thanks to the large overlaps, 25% of a MegaCam field-of-view by design of the L99 observing program.
In general, in any photometric calibration process, the method used to measure fluxes of the calibrating sources should be identical to the method used to measure the flux of the science objects. It is challenging to follow this procedure precisely as described in ? for several reasons, none the least is that CFHTLS is a public survey which addresses many different science objectives, ranging from foreground stars to unresolved galaxies. In some cases, total magnitudes are important; in others, galaxy colors must be accurately measured. Ideally, the calibration process should introduce the smallest possible bias which should be documented and allow users to correct for this bias based on the kind of flux measurement they wish to perform.
A second important consideration comes from the intermediate step used to calibrate the CFHTLS Wide survey. The intermediate L99 photometric images have significantly different characteristics compared to the Wide stacks, as can be seen in Figure 8 which shows the distribution of seeing in L99 calibration images and in actual CFHTLS Wide images; the distribution of image seeing is quite different between the two kinds of images, with very large maximum values reported in the L99 stacks (the L99 were observed under poorer seeing conditions which would have provided out of specifications data for the Wide data set). Moreover, the exposure times are much shorter in the calibration images resulting in larger PSF variations across the field of view due to a less effective smoothing over time of the atmospheric turbulence over the one square degree MegaCam field of view. The method chosen to measure magnitudes scheme should be insensitive to these kinds of variations in exposure time and image quality.

|
Since the calibration is carried out using stars, aperture magnitudes are a natural photometric measurement scheme (and is also fully consistent with the aperture magnitudes scheme used for the SNLS photometric calibration). This is because, in principle, the correction to total flux is the same for all calibrating sources (unlike resolved galaxies which may have vastly differing light profiles).
In this work, as in ? we choose an aperture magnitude where the aperture diameter scales with the image seeing:
 | (1) |
The factor of 7.5 used by ? implies an aperture correction, and in our case we also choose an aperture 20 times larger than the seeing to model and apply such correction to derive the total magnitude of stellar like sources, what we call MAG_IQ20. We call seeing the image quality (IQ) based on measurements made using PSF fitting with PSFex during QualityFITS processing. IQ20 refers to actual measurements on the images using an aperture 20 times larger than the seeing. PSFex is a PSF modelling software developped by Emmanuel Bertin and available on Astromatic17 .
This is motivated by the following considerations:
In extragalactic astronomy, one of the primary scientific aims of the CFHTLS, the pseudo-total MAG_AUTO (?) is the one of the most commonly used estimators of the total flux of galaxies. Ideally, we should use this technique to calibrate our photometry. Unfortunately, our tests have shown that MAG_AUTO measurements do not have the level of precision we require for our photometric calibration. But an alternative is to choose (more stable) aperture magnitudes which matches closely the magnitudes measured by MAG_AUTO.
This is demonstrated in the right and left panels of Figure 9 which shows “Growth curves” for PSF models in the L99 r-band exposures using MAG_SNLS and the measured IQ20 magnitudes to estimate the total magnitudes (left and right panels respectively). If we consider the “true” total flux as the measurement at 40 ×FWHM, the SNLS flux underestimates the total flux by 3% (confirming the analysis from ?). This is only 0.5% when the IQ20 aperture is used. Furthermore, the scatter for the total flux derived using the SNLS aperture magnitude is more than 3 times larger than with the IQ20 aperture (5.1 mmag compared to 1.6 mmag).
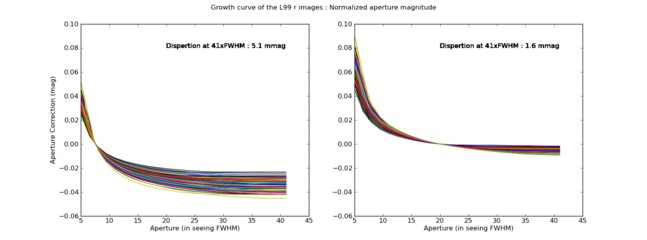
|
Secondly, the choice of magnitude measurement scheme is doubly important when using the SNLS tertiary standards to calibrate the (non-overlapping) L99 calibration fields. For this to work, the flux inside the IQ20 aperture must be as close as possible to a constant fraction of the total flux of the star whatever the shape and size of the PSF.
To test this assumption, we computed an aperture correction defined as the magnitude difference between the measured MAG_SNLS and the measured IQ20 magnitude. This aperture correction is plotted against the image quality in Figure 10. It is important to note that the behavior in the regime of very good image quality clearly departs from a constant aperture correction.
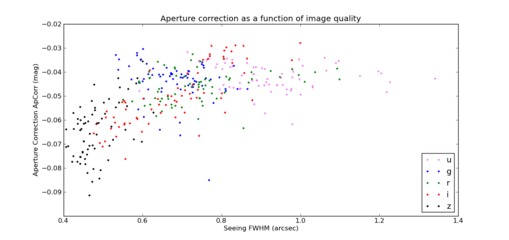
|
For images taken in excellent seeing, the SNLS aperture is too small to capture the same flux versus total flux compared to poorer image quality, which makes the basic SNLS aperture photometry not reliable for our calibration. Figure 11 shows the shape of the PSF for two different FWHM rebined to the same size. One can clearly notice that the overall shape is different : a boxy shape at good IQ due to flux in the spikes and a very symmetrical shape at larger IQ. A tangible explanation of the behavior of the aperture correction at low FWHM is the flux contained in the spikes which scale differently than the bulk of the flux of the PSF.
|
Measuring the flux inside a large aperture of 20 ×FWHM is not a trivial task in the naturally deep CFHTLS stacks where objects are subject to crowding. Instead we chose to model the aperture correction on a per stack basis to go from the robust, but biased, MAG_SNLS to the nearly total magnitude MAG_IQ20.
The use of a master PSF model per image is adopted to ensure a robust estimation of the IQ20 aperture magnitudes. First a pixel-based model of the PSF is constructed using the PSFex software (?) using a large set of stars. From this PSF model (which is produced as a FITS image) the fluxes inside a series of apertures are computed using SExtractor. The aperture correction (ApCorr) is defined as the magnitude difference between the flux inside the SNLS and IQ20 apertures:
 | (2) |
Since photometric rescaling from L99 to the CFHTLS stacks is carried out on only 25% of the MegaCam field of view, a unique PSF model is computed for each of the four quadrants of each L99 image. Despite the PSF variations across a quarter of a MEGACam field of view, a single PSF model is computed : this approximation is motivated by the small variation of the PSF shape and size across the MegaCam field of view compared to the (much larger) variations between the L99 images and the stacks.
The CFHTLS T0007 catalogues offer the MAG_SNLS magnitude since it is the measured value for each source on the image, but it is the aperture corrected magnitude based on the four PSF models for each stacks (and the corresponding four aperture corrections - ApCorr), MAG_IQ20, that ought to be used for any calibration or scientific purposes on point sources.
 | (3) |
|
Deep fields observations bracket L99 observations. Since L99 observations were taken in photometric conditions, the zero-points derived from the comparison of the instrumental magnitudes and the SNLS tertiary standards catalogues should not change. By comparing the zero-points in these pairs of Deep observations (before and after L99 observations) in Table 1, on can see that the MAG_IQ20 is a more stable estimator than MAG_SNLS. stability improves even for Deep images with identical seeing. This result indicates that the scatter in the aperture correction at a given seeing seen in Figure 10 captures real information on the varying PSF shape of identical size.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In conclusion, the variation of the aperture correction with the seeing shown in Figure 10 provides indication that the SNLS flux is not a truly valid proxy of the total flux (measured by the IQ20 aperture photometry) when the images have a large spread in image quality. Our current approach circumvent this obstacle.
The complete CFHTLS-T0007 release (both Deep and Wide) are photometrically calibrated using the SuperNova Legacy Survey (SNLS) tertiary standards catalogs. These catalogs have been produced and release as products of the SuperNova Legacy Survey. They have been made available at CDS in the catalog interface Vizier18 . The detailled description of the production of the catalogs is described in (?).
A summary of the description is reproduced here.
This is the photometric calibration of the SuperNova Legacy Survey (SNLS) three year dataset. The SNLS corresponds to the DEEP component of the larger Canada-France-Hawaii Telescope Legacy Survey (CFHTLS). The SNLS repeatedly monitors four one square degree fields (labeled D[1-4]) with the MegaCam wide-field imager, in the g, r, i and z bands. u-band observations of the same fields are also available, although not formally part of the SNLS dataset.
(...)
The SNLS 3 year calibration relies on the ((?)) standard star catalog. Landolt fields are observed during each photometric night along with the SNLS fields. Zero-points are derived from these observations. Stable and isolated stars are detected on the SNLS fields and selected as "tertiary standards". The calibrated magnitudes of each tertiary standard obtained under photometric conditions are combined to produce a calibration catalog for each SNLS field.
(...)
To interpret the tertiary standard magnitudes as physical fluxes, we need a primary standard, i.e. a star with known MegaCam magnitudes and whose spectral energy distribution has been measured absolutely. The SNLS uses BD+17 4708 whose SED has been measured in Bohlin & Gilliland, 2004, Cat. J/AJ/128/3053 using the HST STIS and NICMOS spectrographs. BD+17 4708 has not been directly observed by SNLS, however, its MegaCam magnitudes were inferred from its known Landolt magnitudes ((?), table 7).
(...)
The u-band observations of the SNLS DEEP fields are not formally part of the SNLS. Nevetheless we give u-band magnitudes for a subset of the SNLS tertiary stars.
The Megacam imager transmission curves are published in the form on tables at CDS : Megacam transmission19 . The filters transmission are shown in figure 13.
|
|
The calibration process for the Deep fields is summarized in Figure 14. In the first step, an object catalogue is produced using SExtractor on the Deep images. This catalogue is then used to produce a PSF model using PSFex. The calibration magnitudes MAG_IQ20 are derived from this catalogue and the PSF model. Next, saturated objects are flagged and are removed. The diagnostic plots used in this procedure are presented in Figure 15. The algorithm first locates the 45 degrees angled thin stellar branch in the MU_MAX (magnitude of the brightest pixel) against MAG diagram (left plot). The saturation level is identified in the MU_MAX axis from the broadening of the distribution along the MAG direction. The resulting saturation level is also plotted in the FLUX_RADIUS versus MAG scatter plot. This estimator is quite robust but can still fail for 1% of the fields for several reasons (such as heterogeneous seeing due to the stacking of images with different image quality or higher number of objects close to the saturation level which blur the determination of the saturation limit). For this reason all plots are manually inspected. Finally, to ensure the cleanest possible calibration sample, an additional 0.5 magnitude margin is subtracted from the MU_MAX magnitude saturation limit.
|
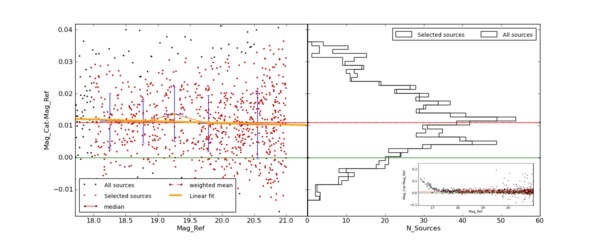
Sources in the Deep stacks are matched with the SNLS standards using a nearest neighbor procedure with a 2′′ matching radius. All stars with a non-zero SExtractor flag are discarded (to avoid blended objects with potentially corrupted photometry). Figure 16 shows the magnitude difference distribution as a function of reference magnitude after matching. The scatter is low, around 1% in average. The 2-σ clipping applied only removes a small fraction of objects (as can be seen in the in the right panel).
The final estimator is the median offset after an iterative two-pass 2σ clipping. A linear regression is used to verify that the estimator does not depend strongly on the magnitude of the selected objects (which would be a sign of systematic biases in our magnitude measurement scheme).
The list of rescaling factors applied to the stacks are given in the Appendix in Table 32. Images are rescaled to keep a final zero-point of Vega 30.0s-1. In a last step, these pixels are scaled to a zero-point of 30.0 in AB. Given a magnitude offset of δSNLS versus the published total magnitude (CAT_SNLS), we get:
 | (4) |
And we can compute a pixel scaling factor of FSNLS as follows:
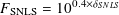 | (5) |
|
The flowchart of the photometric calibration procedure for the CFHTLS Wide stacks is presented in Figure 17. The key aspect of this procedure is the use of the L99 calibration observations to “transfer” the photometry from the SNLS standard stars to the Wide stacks. The L99 fields are observations “bracketed” (proceeded and followed) by an exposure on the Deep survey field closest on the sky to the observed Wide patch. The zero-point of the Deep exposures are calculated in the exact same procedure than described in the previous section. Assuming a perfect stability of the photometric conditions during the series of L99 and Deep observations, the Deep data zero-points are used to calculate the corresponding zero points for the L99 images (taking into account airmass differences).
The zero-point applying to all L99 image taken in the sequence is computed from the mean value of the bracketing Deep fields. In the next step, catalogues with MAG_IQ20 are extracted from both the L99 calibrated images and the Wide stacks. As before, saturated objects are carefully flagged and only stellar objects for which MAG_IQ20 can be reliably measured are selected. The catalogues of overlapping L99-Wide pairs are then matched with the following object selection:
|
From this clean sample rescaling factors are derived from the mean, median or weighted mean. This is illustrated in Figure 18 The resulting median offset, used for the rescaling, is shown as the dashed red line in the main panel of Figure 18. The inset panel shows a linear fit to the bin-averaged statistics (red dots) of the clean sample. Each plot for each L99-Wide pair is visually inspected to ensure a clean calibration sample.
When more than one L99 image overlap with a single Wide stack, the final rescaling factor is a simple average of each separate rescaling factor. The comparison of the individual factors on a Wide stacks is a useful quality assessment of the quality of the calibration and will be discussed in the photometric accuracy section.
For practical reasons, since all objects in a given L99-Wide pair share the same aperture correction, the rescaling offset is computed using SNLS magnitudes (instead of IQ20) and the final rescaling offset includes both the matching offset and the two aperture corrections of the L99 and the Wide catalogues. The final rescaling in magnitude is therefore given by :
 | (6) |
After calibration, image pixels are first rescaled to a zero-point of Vega 30.00 s-1 using the SNLS rescaling factors. In a second step, these pixels are scaled to a zero-point of 30.0 in AB.
The SNLS photometric system is Vega-based using BD+17 4708. We want the CFHTLS releases in a true AB system, in consequence the final processing step converts all images to the AB system by scaling the pixel values using Vega to AB conversion factors. The conversion offsets have been derived by the SNLS Team (Betoule, private communication, 2011); they are listed in Table 2.
?’s calibration system is linked to the HST white dwarf system through the primary spectroscopic standard star BD+17 4708. The Vega magnitudes (at an airmass of 1) for a star of spectral flux density ϕ can be calculated as:
 | (7) |
where Tx0(λ) is the effective filter passband, ϕbd17 is the spectral flux density of the photometric standard BD+17 4708 and mbd17 is the magnitude of BD+17 4708 in the MegaCam instrumental system.
From the definition of the AB system (?), the broadband AB magnitude of a star of SED ϕ(λ) is :
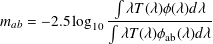 | (8) |
where
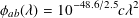 | (9) |
It follows that the AB offsets required to bring SNLS magnitudes to AB system, δab = mab - m|x0, are :
 | (10) |
The pixels in the images are scaled following this relation:
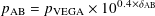 | (11) |
|
|